Consistency in Dice
I have always found it a tad odd that in RPGs you are more or less always just as likely to fail as when you started. Sure the odd stats boost means you technically bumping the probability of you succeeding up, but a critical failure is always just as likely. In reality as you become more skilled at something you become more consistent, more likely to get a similar result. This got me thinking “why can’t RPGs be like this?” and that got me thinking about imperial units.
So we non-Americans love to get all uppity about how metric is better, but I am here to tell you it’s not always true. Sure it makes naming units easier, but what about when I want to describe 1/3 of a meter in millimetres. 333.3 recurring millimetres? YUCK. 1/3 of a foot, however, is just 4”. Elegant. In fact it really speaks to the superiority of base 12 as a whole; its ease at expressing common fractions. But what does this have to do with RPGs and making skills consistent?
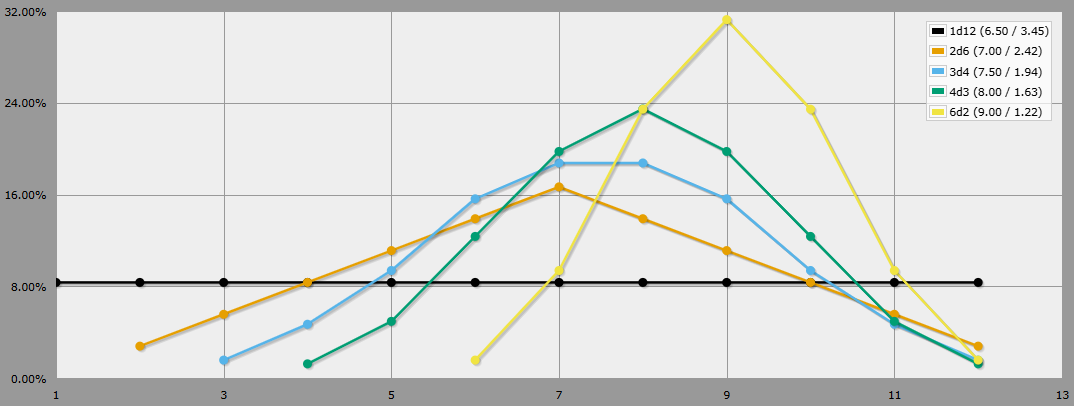
Enter the d12. On its own it is like any other die; each number is just as likely to show up as any other. But we can replace the d12 with 2d6 and suddenly the results form a nice curve. Replace those with 3d4 and the curve gets even nicer. 4d3 (d6/2 if you don’t own any d3s) and that curve is even nicer again. Hell you wanna get freaky? 6d2. Hot damn that is a nice parabola.
There is a small bug that might as well be a feature with this. With each step the lowest possible result gets bigger. In this case I think it helps signify a stat or skill getting more consistent. If there really is a usable game here, I am not too sure, but it is a nice theory and an excuse to screw around on AnyDice. I’ll be back here if anything comes from this, mark my words. Or don’t, I’m not you mum.